107 - Calculate \(\pi\) using Monte Carlo method

Part 1 - Calculate the value of \(\pi\) using the Monte Carlo “rejection” method, by placing a unit circle within a square of side-length 2.

Often people do this more efficiently by using only the 1st quadrant, i.e. one quarter of the circle, but do the full 4 quadrants as in the figure as this will set the stage for Part 2 of the exercise below.

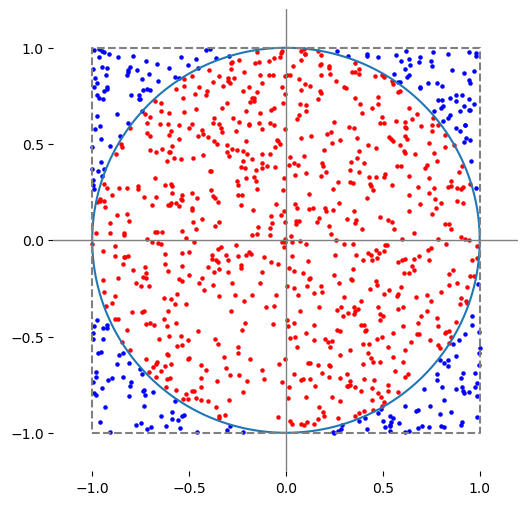
Part 2 - Imagine that the top part of the circle is sliced off horizontally above a given \(y_{crop}\) (where \(-1.0 < y_{crop} < 1.0\)). What is the area of the remaining part of the circle?

Part 3 - Make a plot like the one above for both the simple calculation of \(\pi\) in Part 1 and for the sliced circle in Part 2.

Part 4 - Run the Monte Carlo experiment multiple times with a fixed number of random points (e.g. to calculate \(\pi\)) to get a measure of the variance. Then redo that for several larger values of the number of random points per experiment.